Los 'Huesos de Napier' parecen un dominó, pero son el eslabón entre el ábaco y la calculadora moderna

Publicado el 22/06/2025 por Diario Tecnología Artículo original

El nombre de John Napier puede que no te suene de nada, pero ya te digo que, muy posiblemente, sea una persona que no te caiga bien. Porque lo que puede que sí te suene sea eso de los logaritmos neperianos que a tantos nos traían de cabeza en secundaria. Fue Napier el que definió por primera vez esta función, pero para "compensar", también dio vida a la que podemos considerar como la precursora de la calculadora actual.

Algo llamado ‘huesos de Napier’ que parece un dominó, pero que acercó las operaciones matemáticas a más gente.

John Napier. A este escocés le interesaban muchas cosas. Su familia estaba más que asentada y, como buen hijo de pudientes, asistió a la Universidad de Saint Andrews a los 13 años. No duró mucho, pero no porque quisiera dejar los estudios, sino porque se fue a otras universidades de Francia, Italia o Flandes. Se pasó la vida viviendo de castillo en castillo, donde dio rienda suelta a varias de sus pasiones.

Un mago (pero no de los números). Era protestante y considerado un mago negro por sus vecinos. También era un tipo ingenioso. Cuando las palomas se comían su grano, decidió esparcir semillas mojadas en alcohol por el campo y, con las palomas ‘anestesiadas’ y sin poder volar, se dedicó a capturarlas. Como siempre, y más cuando hablamos de este tipo de historias con varios siglos a sus espaldas, la imaginación y la exageración hacen su trabajo, pero lo que es innegable es que a Napier le gustaba resolver problemas.

Su mayor aporte es el comentado Mirifici Logarithmorum Canonis Descriptio en el que definió los logaritmos actuales en 1614, pero antes y después publico otros tratados del campo de las matemáticas en los que exploraba la forma de simplificar las tareas de cálculo. Y no sólo teorizó sobre las mismas o impulsó la coma en los decimales: creó herramientas para solventar esos cálculos de forma más sencilla.

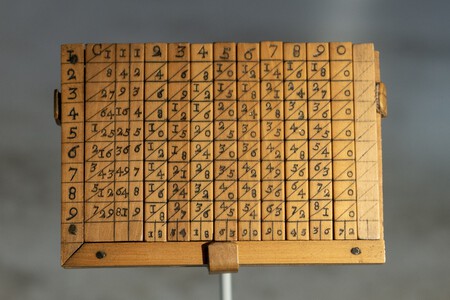
El nuevo ábaco. Desde que necesitamos resolver problemas matemáticos, la humanidad ha buscado el modo de apoyarse en herramientas. Así surgieron los ábacos, o los quipus con los que se podían hacer operaciones sencillas como sumas, restas y multiplicaciones. Con unas matemáticas más complejas, había que dar una vuelta al sistema, y Napier se sacó de la manga su nuevo ábaco, o una protocalculadora.

Los huesos de Napier. En 1617, poco antes de morir, el matemático inventó una herramienta manual enfocada a facilitar algunas operaciones más complejas, como la multiplicación y la división, pero también las raíces cuadradas. Se trató de un conjunto de varillas rectangulares en las que se grababan las tablas de multiplicar, además de un tablero con huecos para las varillas y con las cifras del 1 al 9 dispuestas en forma vertical en la parte izquierda.

Al colocar estas varillas una al lado de las otras, se reducían las operaciones de multiplicaciones y divisiones a simples sumas y restas, respectivamente. Originalmente, se fabricaron en metal o madera, sobre todo, pero también se podían construir estas varillas en marfil, y un juego completo incluía 10 varillas para representar los números del 0 al 9.

¿Qué? Vale, como ocurre con las matemáticas, veamos ejemplos. Uno muy sencillo se ve con la multiplicación, porque así no necesitamos memorizar las tablas. Si queremos saber cuánto es 2 x 6, simplemente buscamos la fila 2 de la derecha y la varilla que empieza por 6 y vemos qué número hay en el cuadrante: el 12. Si queremos hacer un 8 x 8, repetimos el proceso y vemos que tenemos un 64.

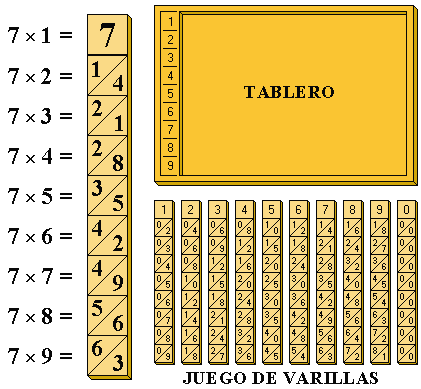
Si hacemos una operación más compleja, como 46785399 x 7, colocamos las varillas correspondientes a ese número (la que empieza por 4, la que comienza por 6 y así sucesivamente) una al lado de la otra de izquierda a derecha y nos fijamos en el número que sale en la fila 7, que es por la que queremos multiplicar.

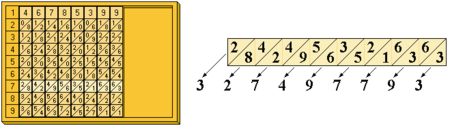
Ahora, de derecha a izquierda, vamos colocando los números que aparecen unidos en la casilla diagonal: 327497793. Matemáticos posteriores mejoraron el sistema al crear un tablero con una inclinación de 65º que mejoraba la identificación visual de esa fórmula, pero los ‘huesos de Napier’ fueron una revolución al acercar ese cálculo matemático más complejo a personas sin estudios superiores. Lo único que había que aprender era la regla de la multiplicación y la división con el sistema del tablero.

Una joya. Muriendo en 1617, es complicado que Napier viera la trascendencia de su obra tanto teórica como práctica, pero hoy sus fundamentos logarítmicos se siguen empleando, también la coma de los decimales, un cráter lunar lleva su nombre y ese ábaco neperiano es una de las joyas del Museo Arqueológico Nacional de Madrid.

No se sabe quién lo fabricó, pero se trata de un estuche de madera de un tamaño considerable con 30 cajones en los que se guardan las fichas de los dos ábacos diseñados por el matemático. Uno de ellos formado por 60 varillas numeradas construidas en hueso y el segundo, llamado 'promptuario', compuesto por 300 fichas lanas numeradas y perforadas para realizar multiplicaciones.

Y es como una megachuleta, ya que en las puertas de las cajas se encuentran las primeras potencias de los números dígitos, los coeficientes de las primeras potencias del binomio y los datos numéricos de los poliedros regulares. Curioso que las calculadoras, aparte de ser objetos con un fin concreto, se han convertido en algunos casos en auténticas obras de arte. Que se lo digan a la Divisumma.

Imágenes | Maksim, Willy, Luis García, Kim Traynor, The wub

En Xataka | El "ordenador" de hace 2.000 años nos fascina desde hace décadas.  Un nuevo estudio apunta que podría no haber servido para nada

utm_campaign=22_Jun_2025"> Alejandro Alcolea .